Selected Research Work
Overview
These days, there is an unprecedented amount of data available. As a result, tremendous opportunities have been created for Machine Learning-based data analysis and multiple successful algorithms and tools have been developed to resolve various challenges that accompany these data. However, many real-world datasets are imbalanced, which poses a significant and difficult conundrum: real-world data is often heavily imbalanced, and classifiers trained on imbalanced data strongly favor the majority class---leading to a gap in accuracy when predicting particular events based on large quantities of data where those instances are relatively rare. These types of rare events buried amongst masses of data could include things like the relatively few heart attacks or strokes experienced by the minority versus thousands of other healthy patients, or the relatively infrequent instances of financial fraud, space shuttle failure, or criminal conduct caught on surveillance, as compared to multitudinous data showing no such events.
Selection Framework for Handling Imbalanced Data in Supervised Learning: A Semi-Supervised Learning Approach
Introduction
Many sampling methods which have been presented in recent years. Most of these studies report the average results amongst a set of imbalanced datasets. However, looking at each set individually, it is clear that there is no method that performs best as compared to all other methods for all datasets. Therefore, given an imbalanced dataset, can we ask the following questions: Which sampling method should be used? Which method is the best?
There is no direct answer. As reported by many studies, there is no method that outperforms all others in all given datasets. My current work aims to establish a framework using semi-supervised learning to help determine the most suitable way to select a sampling method for any given dataset.
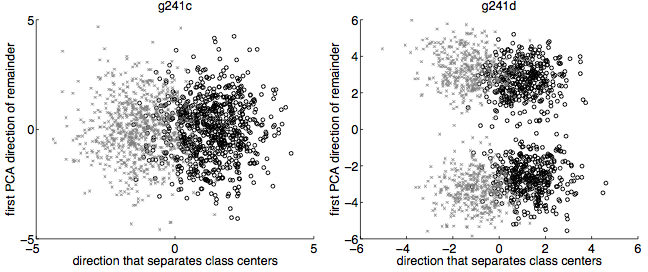
We established rules to help us choose the proper sampling method to balance and refine the dataset to establish a well-defined training set. Our results validate our framework where we achieve better or comparable results to other state-of-the-art sampling methods by applying the rules and following the selection framework.
Bassam Almogahed, Ioannis A. Kakadiaris: Novel Framework for Supervised Learning in Imbalanced Data: A Semi-Supervised Learning Approach. Machine Learning. 2015 (under review)
Under-Sampling Via Semi-Supervised Learning
Introduction
My other work tackles the problem of reducing the size of an unbalanced dataset without losing important information. A successful under-sampling technique retains all minority examples and prunes only unreliable majority examples, which could be: noisy, or located too close to the boundary between the minority and majority regions, redundant, or borderline examples from the majority class in the overlapping regions between classes. Any performance degradation is caused mainly by the overlap between the imbalanced classes. More recent experiments on artificial data with different degrees of overlapping have demonstrated that overlapping is more important than the overall imbalance ratio.
My work takes advantage of the fact that under-sampling (US) and semi-supervised learning (SSL) can each be viewed as possessing the common goal of drastically compressing data without losing the underlying information. All learning strategies must therefore be based on a belief in the hidden inherent simplicity of relationships P(A|B). We map this concept on to under-sample the data using SSL. The targeted datasets are all initially labeled, but they are yet imbalanced. With US, we create unlabeled data by stripping the labels from the majority class instances. As such, the problem is transformed from supervised to semi-supervised. It is then solved to identify and remove borderline instances, especially those that overlap largely with the minority instances.
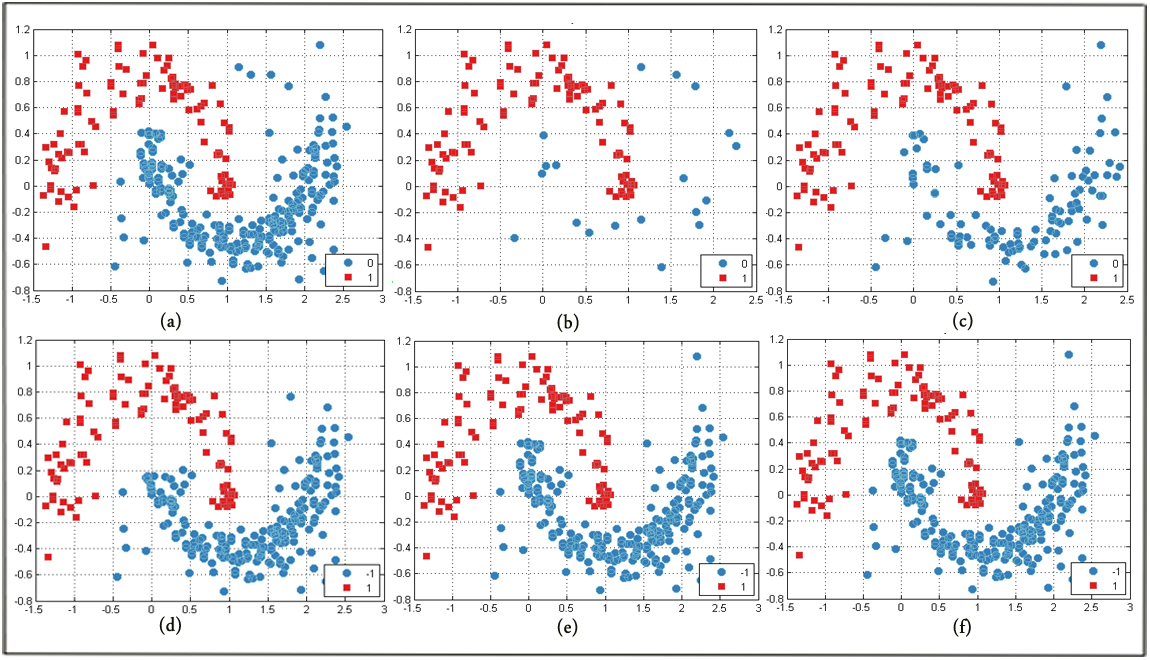
Our results corroborate our prediction that US-SSL algorithms produce significantly better or equivalent results as compared to other state-of-the-art US algorithms.
B. A. Almogahed and I. A. Kakadiaris. Empowering imbalanced data in supervised learning: A semi-supervised learning approach. In Proc. International Conference on Artificial Neural Networks, Hamburg, Germany, Sep 15 2014.
Synthetic Over-Sampling for Imbalanced Data
Introduction
My recent work explores the creation technique of synthetic data in a more consistent and robust manner. Over-sampling approaches have improved learning with respect to data distributions on imbalanced datasets by reducing the bias of class distribution and adaptively shifting the decision boundary to focus more attention on instances, which are difficult to learn. Our studies show that there are two objectives that an effective over-sampling method needs to accomplish: (1) creating representative synthetic data, and (2) reducing noise. Over-sampling algorithms are only able to accomplish one of these objectives well, but are unable to combat both the representative synthetic data issue as well as the noise problem.
Likewise, unimodal systems generate heterogeneous score distributions across probes.
Score normalization methods compensate for such effects by standardizing the score distributions.
While such methods are frequently used by multi-modal systems, they are less widespread in unimodal systems.
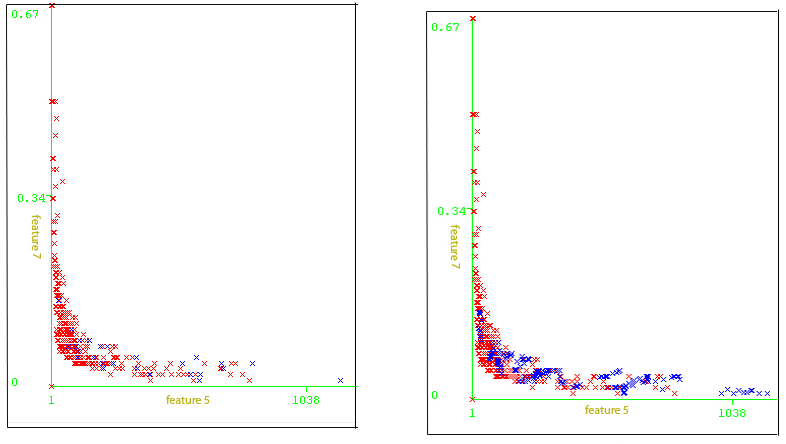
Overview
Our approach has several significant advantages over other approaches. First, it does not operate on prior assumptions---the new minority samples are actually more representative of the minority class. Second, it is able to attain high accuracy for the minority class without jeopardizing majority class accuracy. Finally, it can successfully obtain representative synthetic instances while generating a very small degree of noise.